6. How is it Supposed to Work?

Needless to say, most astrologers make no attempt at all to explain how or why the positions of the Sun, Moon and planets should affect people’s personalities or determine the course of their lives. Obviously, there is no possible explanation, as the entire concept is left over from the days when the planets were thought to revolve around the Earth attached to crystal spheres, and is all based on mysticism and magic. A few of them, however, have made pathetic attempts to justify it, based on half-baked ideas of “gravitational attraction of the planets on the fluids in the body”, and the like – again without any attempt to explain why such attraction ( even if it had any noticeable effect, which it doesn’t ) should affect people’s personalities. All they succeed in doing is demonstrating their own ignorance of even the most elementary physics.
Here, I’ll look at the ways in which astrology could be claimed to work, and show conclusively that it doesn’t.

6.1. The forces of nature

Let’s suppose for a moment that the Sun, Moon and planets do, as astrologers claim, somehow exert some kind of “influence” on every human being. What could this “influence” be? Presumably, it must be due to some kind of force.
In physics, there are four known forces which any objects, or concentrations of matter, can exert upon each other. Two of these are familiar to all of us – gravity and the electromagnetic force. The other two are less well-known, except to physicists; they are called the “strong” and “weak” nuclear forces, and are what holds the nuclei of atoms together.
All forces are strongly dependent on the distance between objects; the further apart, the weaker is the force. The strong and weak forces are significant only at the scale of atoms and subatomic particles; even the strong force ( “strong” is a relative term, simply meaning that it’s much stronger than the “weak” one ) is really so weak that its effect is negligible at distances of more than a few millionths of a millimetre. So for any macroscopic objects, let alone planets, their effect is, to all extents and purposes, non-existent. So we can discount these forces immediately.
So we are left with gravity and electromagnetism. Both of these obey the inverse square law, which means they diminish with the square of the distance apart, if the distance is doubled, the force diminishes by a factor of four, and so on. I’ll say more about that in Section 6.2. Gravity depends on mass, and electromagnetism on electric charge.
The problem with the latter is that large objects, such as planets, don’t have any overall electric charge. Charge comes from subatomic particles, such as protons and electrons, and on any macroscopic scale, these exist in equal numbers and cancel each other out.
Some of the planets – but not all of them – do have magnetic fields; that of the Earth is what makes a magnetic compass work. But thanks to the inverse square law, their effect on the Earth is negligible. Jupiter, in particular, has an immense magnetic field, many times stronger than that of Earth – but it’s also a long way away.
The Sun, however, has a vastly greater magnetic field than even that of Jupiter. This does directly affect us here on Earth; magnetic storms on the Sun blast out intense streams of charged particles into space, which can travel as far as the Earth and beyond. When these interact with the Earth’s own magnetic field, they cause aurorae – the Northern and Southern Lights. Occasionally, they can have far more serious effects, such as damaging satellites in Earth orbit, or even knocking out power grids.
So it’s remotely conceivable that electromagnetism could have some sort of effect on the human body, which could explain astrology. If this was the case, then the Sun would be by far the dominant force, and any effects of the planets would be miniscule in comparison. But this contradicts astrologers’ claims that the planets have significant effects.
So that leaves us with gravity. The planets do, of course, have plenty of mass – but again, they are a long way away. The Moon has much less mass – only 1/81 of that of the Earth – but it’s also much closer to us. It’s very easy to show – and I’ll do so in detail in Section 6.2 – that the gravitational influence of the Moon is orders of magnitude greater than that of any of the planets.
So if electromagnetism was the cause, than the Sun would be by far the dominant factor in astrology – but it isn’t. If gravity was the cause, than the Moon would be by far the dominant factor in astrology – but it isn’t. So we can safely conclude that the astrologers’ imaginary “influence” is not caused by any of the known forces of nature.
The only way out for them is to claim that it’s caused by some other mysterious force or effect, which is not known to science! I’ll examine that hypothesis in Section 6.5 – but first, I’ll look in more detail at gravity.

6.2. Gravity and the inverse square law

This is where we have to go into a little physics and maths – but don’t worry; we only need to consider one equation!
We all know, of course, that the gravitational attraction between the Earth and the Moon does have significant effects; it’s what causes the tides! One of Britain’s best known astrologers, Russell Grant – a man who could be described as absurdity personified – has tried to use this fact in a truly pathetic attempt to justify astrology. He once stated on TV, “The Moon exerts a gravitational pull on the water in the oceans, to cause the tides – so it must have some effect on the fluids in the body!” Naturally, he made no attempt to say how or why any “gravitational pull” on the fluids in the body should influence a person’s personality – or why, given that that pull is always present and ever-changing at every moment of a person’s life, its particular configuration at the moment of birth should be so important!
I can only assume that Mr. Grant never learned even the most elementary physics at school, and that he has never even heard of the inverse square law!
Firstly, it’s a complete fallacy to say that one object “exerts a gravitational pull on” another. It does not! What actually happens is that every two objects exert a mutual gravitational pull on each other, which depends upon both of their masses!
The Law of Gravitation, as formulated by Sir Isaac Newton, states as follows: “Every object attracts every other object, with a force which is directly proportional to the product of their masses, and inversely proportional to the square of their distance apart.”
Note - the force is proportional to the product of their masses – that is, both masses multiplied together! So the mutual gravitational attraction between the Moon and the water in the Earth’s oceans is proportional to the masses of both. The mass of fluid in a human body is very much less than the mass of water in the oceans – by a very rough calculation, it’s smaller by a factor of about 5 x 10¹⁹ ( that’s a 5 followed by 19 zeroes, or 50 million million million ) – so the attraction between it and the Moon is correspondingly smaller. In other words, it’s absolutely miniscule. Duh!!!
The Law of Gravitation can be expressed mathematically as follows. The force F, mutually exerted between two bodies of masses m₁ and m₂, separated by a distance r, is given by

F = G m₁ m₂ / r²

where G is a constant, called the Universal Constant of Gravitation. If the masses are expressed in kilograms, the distance in metres and the force in newtons, the value of G is 6.67 x 10^-11 Nm²kg^-2.
The r² on the bottom of the equation gives us the inverse square law. If the distance apart is doubled, the force is reduced by a factor of four; if the distance is multiplied by ten, the force is reduced by a factor of 100, and so on. So it’s easy to see that the distance apart soon dominates over the masses.
Now let’s look at some numbers, with regard to the Moon and planets. The masses of those bodies, and their distances from Earth, can be found in any decent astronomy textbook, or in Wikipedia, if you want to check the maths for yourself.

6.3. Gravity – the Moon and planets

Let’s consider the gravitational force between an object on the Earth’s surface and various astronomical bodies. In the equation above, m₁ is the mass of the astronomical body, and r is its distance from Earth. m₂ is the mass of the object on Earth, which I’ll call X – be it a human being or anything else. It doesn’t matter what that mass is, as it’s the same in each case. At this point, we don’t actually need to calculate what the force is; I’m simply going to calculate the ratio of the forces exerted by different bodies, by comparing their masses and distances.
I’ll start with the Moon. Its mass is 1/81 of that of the Earth ( astronomy books often state the masses of other Solar System bodies as multiples of that of Earth ), and its mean distance from Earth is roughly 382000 km. Most of the other planets have much more mass than the Moon, but they are also very much further away.
The nearest other planet to Earth is Venus. Its distance from Earth varies by about a factor of six, depending on where the two planets are in their orbits, but the closest it comes to us is about 42 million km – that’s 110 times as far as the Moon. Its mass is 0.82 times that of Earth, or about 66 times that of the Moon. Now remember that the gravitational force is proportional to the body’s mass, and inversely proportional to the distance – so to compare the gravitational force between Venus and X with that between the Moon and X, we multiply by the ratio of their masses, and divide by the square of the ratio of their distances. That’s 66 / 110² = 0.0055. So even when Venus is at its closest, its gravitational influence is only about one two hundredth that of the Moon.
Now let’s consider Jupiter, the biggest of the planets. It has much more mass than Venus, but it’s also much further away – and as we’ve just seen, distance is the more important factor. Jupiter has 318 times the mass of Earth, or nearly 26000 times that of the Moon. At its closest, its distance from Earth is 627 million km – 1640 times that of the Moon. So the ratio of gravitational forces in this case is 26000 / 1640² = 0.0097; the gravitational influence of Jupiter is only one hundredth of that of the Moon!
So we see that the gravitational influences of both the closest planet and the biggest are tiny, compared to that of the Moon. Those of the other planets are even smaller; the influence of the Moon on our object X is more than fifty times greater than that of all the other planets combined!
So how about the Sun? Obviously, its gravitational influence is far greater than that of the Moon or planets, as it’s the body around which the rest of the Solar System orbits. It’s 390 times as far away as the Moon, but has 27 million times its mass – so in this case, it’s the mass which wins, and we find that the Sun’s gravitational influence is 180 times greater than that of the Moon. But then, the Sun isn’t usually mentioned in astrologers’ horoscopes, is it? The position of the Sun at the time of your birth determines your so-called “star sign” ( also called a “sun sign” ), but it’s the Moon and planets, and their changing positions in the Zodiac, which are supposed to influence day to day events.
We can therefore conclude that if gravity was the “influence” behind astrology, then the influence of all the planets would be insignificant, compared to that of the Moon – but according to astrologers, that isn’t the case. And the influence of the Sun would vastly dominate even that of the Moon – but that isn’t mentioned at all!

6.4. Gravity – things closer to home

According to astrology, the positions of the Moon and planets at the moment of birth are vitally important for determining a person’s personality. So whatever the “influence” of those bodies is supposed to be – whether it’s gravity or anything else – the particular configuration of those “influences” at the moment of birth is supposed to be all-important.
( Why is the moment of birth supposed to be so important, anyway? Not only are those supposed “influences” always present and always changing, throughout a person’s life; they are also present during the nine months before birth! The ancients believed that birth was the “magic” moment at which life began, but now we know differently. So why is the moment of birth so important, rather than the moment of conception? The simple answer, presumably, is that most people know the exact time and place of their birth, but it’s somewhat more difficult – and probably embarrassing – to determine the time and place of your conception! )
So let’s continue to assume that the “influence” is due to gravity, and consider the gravitational forces which act on a baby at the moment of its birth. As I’m about to prove, the doctor who delivers the baby exerts a greater gravitational pull on it than do most of the planets! It’s time to do a little maths, and put some numbers into the equation which I showed earlier. Let’s remind ourselves of the equation:

F = G m₁ m₂ / r²

where the constant G has a value of 6.67 x 10^-11 Nm²kg^-2.
In each of the calculations which follow, m₁ is the mass of the “attracting” object, m₂ the mass of the baby – which I’ll assume is 3 kg – and r their distance apart.
First, let’s consider the Moon. In this case, we have
m₁ = 7.4 x 10²² kg
m₂ = 3 kg
r    = 382000 km = 3.82 x 10⁸ m

So F = ( 6.67 x 10^-11 x 7.4 x 10²² x 3 ) / ( 3.82 x 10⁸ )² = 1.03 x 10^-4 N

( 10^-4 means one divided by 10⁴, or 0.0001 – so the force here is 0.000103 N, or just over one ten thousandth of a Newton. )
Now let’s consider Venus, at its minimum possible distance of 42 million km. In this case, we have
m₁ = 4.9 x 10²⁴ kg
m₂ = 3 kg
r    = 4.2 x 10⁷ km = 4.2 x 10¹⁰ m

So F = ( 6.67 x 10^-11 x 4.9 x 10²⁴ x 3 ) / ( 4.2 x 10¹⁰ )² = 5.56 x 10^-7 N

Now for the doctor. Let’s assume that he has a typical mass of 75 kg ( a bit less if the doctor is a woman! ). For the purpose of the calculation, any object can be considered as a point mass, concentrated at its centre of mass, or centre of gravity – so the distance r is that between the centres of mass of the doctor and the baby. At the moment of birth, that distance is pretty small – say about 30 cm, or 0.3 m. So we have
m₁ = 75 kg
m₂ = 3 kg
r    = 0.3 m

So F = ( 6.67 x 10^-11 x 75 x 3 ) / 0.3² = 1.67 x 10^-7 N

We can see, therefore, that the gravitational influence of the doctor on the baby is roughly a third of that of Venus. This means that it’s about a sixth of that of Jupiter – which I showed earlier to be about twice that of Venus – and significantly greater than that of any of the other planets. It’s less than 1/500 of that of the Moon – but once again, astrologers claim the influence of the planets to be just as important as that of the Moon, don’t they?
Note that in those calculations, I considered Venus at its closest. But its distance varies greatly; at its furthest, when it and the Earth are at opposite sides of their orbits, it’s six times further away, and the gravitational force between it and any object on Earth is reduced by a factor of 36. Most of the time, its distance is somewhere in between. So we can conclude that in most cases, the gravitational influence of the doctor on the baby is greater than that of any of the planets except Jupiter.
But then, we have only considered the doctor. There are also other people in the delivery room – at least one nurse, and usually the mother’s partner. If we assume that they are each about a metre away, then their gravitational influences on the baby will each be about a tenth of that of the doctor.
Then there are all the other objects in the room. The bed, or birthing chair, probably exerts a similar force to the doctor, as it’s of comparable or greater mass, and the distance between centres of gravity is similar. There will also be various machines and instruments in the room, which are a couple of metres away, and have greater masses. All these calculations have been done in great detail by Moriel Schottlender at www.smarterthanthat.com/astronomy/astrology-a-practical-test-objects-that-affect-you-at-birth.
Here, we have only considered the mutual gravitational force, as if it acts through the bodies’ centres of mass. But what about the tidal effect? This is the difference between the gravitational forces experienced by opposite sides of an object. The length or width of a baby’s body is infinitesimal, compared to its distance from the Moon or planets, but it’s a significant fraction of its distance from the doctor’s centre of mass. It can be easily shown, by a little more maths using the same equation, that the tidal force experienced by the baby due to the doctor is several million times greater than that due to the Moon, and billions of times greater than that due to any planet.
So there you have it, folks – conclusive proof that Mr. Grant’s idea about “gravitational pull on the fluids in the body” is utter drivel! If astrology was driven by gravity, then the positions of the people and machines in the delivery room would be at least as important as those of the planets!

6.5. An unknown force?

Needless to say, most astrologers don’t actually claim that gravity is the explanation. They don’t attempt any kind of scientific explanation at all, as they are not concerned with the scientific method, or the principle of cause and effect, but with mysticism and something akin to magic. Some of them claim that the planets exert some mysterious “force” or “influence”, which is still unknown to science. If that’s the case, then their hypothetical “force” must have some very strange properties!
For starters, unlike all the forces known to physics, it doesn’t obey the inverse square law! According to astrologers, the “influence” of the planets depends only on their direction in the sky – i.e. which “sign” of the Zodiac they are in – and not on their distance from the Earth. That’s hardly surprising, since the ancients didn’t know that their distances change! But for the three nearest planets, their distances vary hugely, with the relative positions of them and Earth in their orbits.
Fig. 2 shows the orbits of Earth and Mars, drawn to scale. ( The orbits are really ellipses, but I’ve drawn them as circles for simplicity. They are in fact not far from circular. )

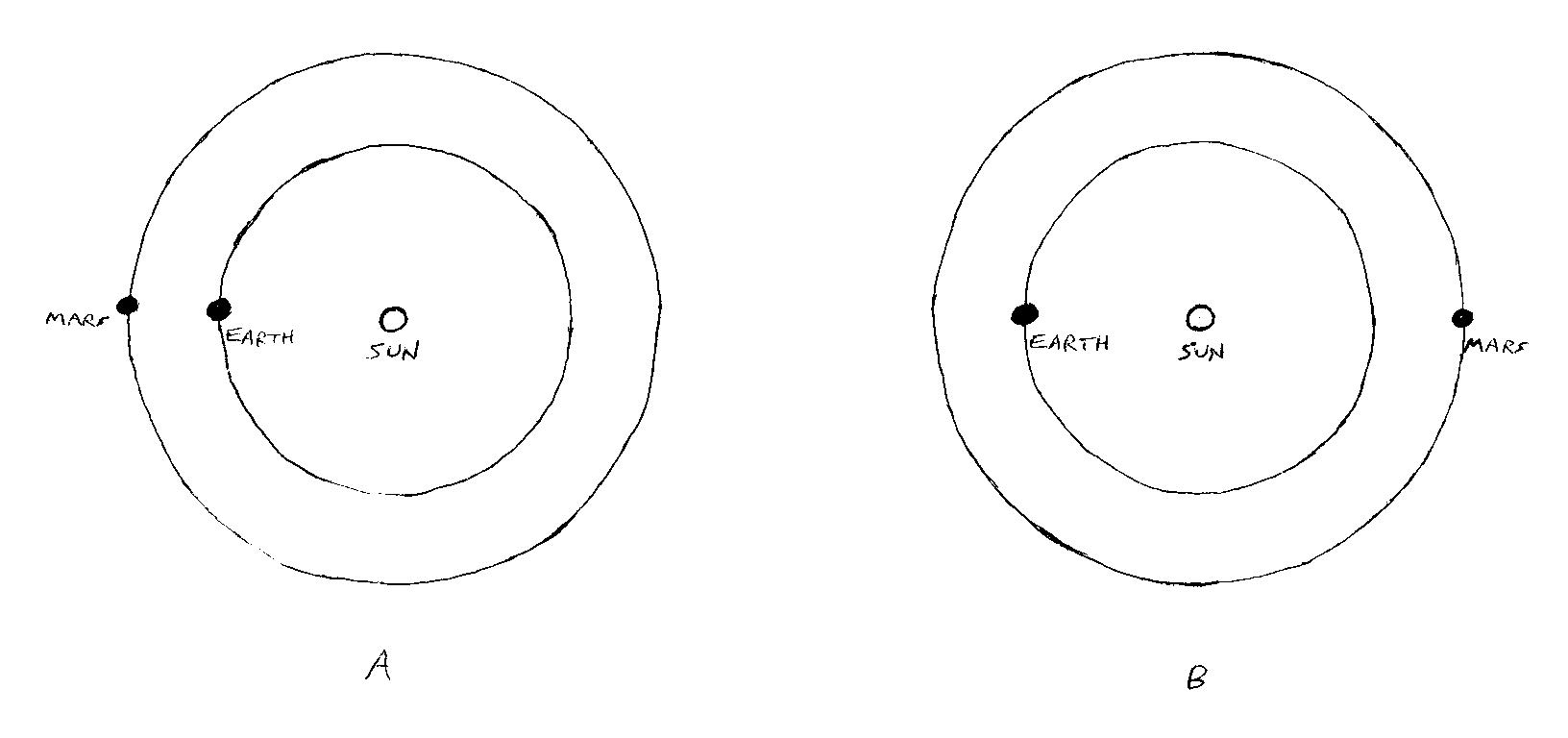
Fig. 2

As you can see, when Mars is at its furthest from us, as shown in diagram B, it’s five times as far away as it as at its closest, as shown in diagram A. Therefore, the effect of its gravity, or any inverse square law force, is diminished by a factor of 25.
Similarly, the distance of Venus from us varies by a factor of six, and that of Mercury by a factor of two.
But none of this matters to astrologers. Their horoscopes simply depend on whether Mars is in Taurus, or in Gemini, or whatever, and don’t consider whether it’s at its closest to us, or far away on the other side of its orbit. So their supposed unknown “force” apparently does not diminish with distance.
This mysterious “force” also has another bizarre property. As I stated earlier, it apparently has no effect during the nine months before birth – so it seems that a baby is somehow “shielded” from it while it’s in the womb! So this “force” is propagated across millions of kilometres of space, through brick or concrete walls ( most babies are born inside buildings, after all ), and even through the entire Earth ( it doesn’t matter whether any given planet is above the horizon at the place of a baby’s birth, or hidden on the opposite side of the Earth ) – yet it’s somehow “stopped” by a couple of centimetres of flesh and muscle!
Furthermore, if this “force” is independent of distance, then why are only the planets of the Solar System supposed to affect our personalities? Why are we not affected by the “influence” of other stars – which, after all, are vastly bigger than planets? There are a hundred billion stars in our Galaxy alone – and the fact that most of them are thousands of light years away should not matter.
Even if we conveniently assume that this “force” is somehow only exerted by planets, and not by stars, this still doesn’t get astrologers off the hook – because other stars also have planets! As recently as twenty years ago, we had no direct evidence of any planets of other stars - but now we know of over a thousand of them, and new ones are discovered by the week. And that’s only within the Sun’s relatively close neighbourhood; we can now safely assume that the majority of stars have planets. So why don’t we feel the “influence” of all those billions of planets?
All this, remember, is a logical consequence of astrologers’ own assumptions. We can conclude that, just like the gravity arguments, those about mysterious unknown “forces” are utter drivel.

6.6. How many planets are there anyway?

Finally, even if we still arbitrarily assert that only the planets of our own Solar System matter, we still have a big problem; for most of the history of astrology, some of those planets were not even known to exist!
Five of the planets – Mercury, Venus, Mars, Jupiter and Saturn – have been known since ancient times; of course, the ancients didn’t think of the Earth as being one. But the most distant two or three, depending on your point of view, are too faint to be visible to the naked eye, and so were not discovered until after the invention of the telescope. Uranus was discovered in 1781, Neptune in 1846 ( its existence having been predicted, due to its gravitational effect on Uranus ), and Pluto as recently as 1930.
But today, astrologers always include Uranus, Neptune and Pluto in their horoscopes, and have even made up aspects of people’s lives for which they are supposedly responsible. So if you assume astrology to be valid, it follows that every horoscope ever written before 1930 was inaccurate and/or incomplete! Conversely, why were astrologers not able to deduce the existence of those planets, due to the systematic errors in their own predictions?
But wait – how many planets are there in the Solar System anyway? This is very much a matter of definition, and since 2006, Pluto has no longer been officially defined as one. Astrologers seem to have missed that news, as they still include it.
When Pluto was discovered in 1930, it was naturally considered to be the ninth planet, as it was the only known object further from the Sun than Neptune. It was also initially thought to be quite big, perhaps bigger than Earth – but over the years, estimates of its size grew steadily smaller, and we now know that it’s smaller than the Moon. ( It does, however, have a satellite, called Charon, which is half its own size. )
Then, during the 1990s, astronomers began to discover many more small bodies in the region beyond the orbit of Neptune. Hundreds of them are now known, and there are probably thousands or even millions more yet to be discovered, in what has become known as the Kuiper Belt. Pluto turned out to be just one of a huge number of Kuiper Belt objects ( KBOs ); it simply happened to be the biggest. Many astronomers proposed that Pluto should no longer be classified as a planet – though some still insisted that it should be, for reasons which had more to do with sentiment than science.
Then in 2003, came the discovery of the KBO now known as Eris, which turned out to be bigger than Pluto; Pluto had lost even the distinction of being the biggest! It followed that if Pluto was still considered a planet, then so must Eris be, and vice versa. A handful of other KBOs are also now known, which are not all that much smaller.
In 2006, the International Astronomical Union adopted a formal set of definitions for Solar System bodies, with the result that Pluto is no longer defined as a planet, but has been “relegated” to the new category of a “dwarf planet”. ( A dwarf planet is a body which is big enough for its gravity to have moulded it into a roughly spherical shape, but which doesn’t gravitationally dominate the vicinity of its orbit, as true planets do. ) The set of dwarf planets also includes Eris and eight other large KBOs – two of which have yet to be given formal names – and also Ceres, the biggest of the main belt asteroids, which has been known since 1801.
So why don’t astrologers’ horoscopes now consider the influence of Ceres, Eris, Makemake, Haumea, Quaoar, Sedna, Orcus and Salacia?

Previous page Next page

Return to Contents